(The following questions are refered to in the solutions video as Part A, Part B, Part C, Part D, and Part E of Question 3.)
As you observed in the previous two problems, forward and backward Euler both make errors. Combining the two of them, however, can be surprisingly effective. Implement a solver that averages a forward and backward Euler step:
![\vec{x}(t+\Delta t)=\vec{x}(t)+\frac{\Delta t}{2}\bigg[f(\vec{x}(t))+f(\vec{x}{__F}{__E}(t+\Delta t))\bigg]](/gif.latex?%5Cvec%7Bx%7D%28t+%5CDelta%20t%29%3D%5Cvec%7Bx%7D%28t%29+%5Cfrac%7B%5CDelta%20t%7D%7B2%7D%5Cbigg%5Bf%28%5Cvec%7Bx%7D%28t%29%29+f%28%5Cvec%7Bx%7D%7B__F%7D%7B__E%7D%28t+%5CDelta%20t%29%29%5Cbigg%5D)
Here  is the result of applying one step of the forward Euler algorithm starting from
is the result of applying one step of the forward Euler algorithm starting from 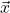 with time-step
with time-step 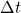 . This method averages the slope at that point with the slope at the originial point and uses that averaged slope to move forward. This is sometimes called the trapezoidal method in the literature.
. This method averages the slope at that point with the slope at the originial point and uses that averaged slope to move forward. This is sometimes called the trapezoidal method in the literature.

